Влияние ветра на полет пули Влияние ветра на полет пули Влияние ветра на полет пули
В книге "Спортивная стрельба из винтовки": Руководство для стрелков и тренеров" Б. Пуллэма и Ф. Т.Хейненкрата есть следующая информация: После того как пуля покинула ствол, ее направление изменяют две основные силы - тяготение и ветер. Сила тяготения начинает действовать, едва пуля покинула ствол. Таким образом, пуля, выпущенная из винтовки в направлении, параллельном земле, упадет на землю с той же скоростью и через такое же время, что и пуля, просто упавшая на землю с этой высоты. Если уж мы заговорили о практических вещах, то напомним, что сила притяжения - величина постоянная и всегда отклоняет пулю вниз в вертикальном направлении, которое всегда строго определенно. Поскольку это так, стрелку не нужно вносить никаких изменений в прицел. Однако сила и направление ветра непостоянны и заранее не заданы, а потому доставляют большинству стрелков массу неприятностей. Влияние ветра на полет пулиПопутный или встречный ветер (действуя совместно с силой тяготения) приводит к необходимости внесения в прицел только вертикальных поправок. Если пуля летит строго навстречу ветру, ее скорость уменьшается, и пробоина в мишени будет расположена ниже. Если пуля летит по ветру, ее скорость возрастает; для действия силы тяготения остается меньше времени, и пробоина в мишени будет расположена выше. Но на стрельбищах практически никогда не бывает строго встречного или попутного ветра. Обычно ветер дует наискось или поперек линии огня и, как мог убедиться каждый, изменяет направление полета пули. Сильнее всего влияет горизонтальный поперечный ветер - при этом пуля во время полета отклоняется вправо или влево. Этот ветер вызовет также и некоторое вертикальное смещение, зависящее от направления вращения пули и направления ветра. Вращение пули приводит к образованию зон вакуума и повышенного давления, поэтому влияет на траекторию полета гораздо больше, чем мы полагаем. (Точно также вращение бейсбольного мяча вызывает искривление и другие изменения его траектории после удара хорошего игрока.). Непостоянство ветра имеет двойной характер - ветер непостоянен и во времени, и в пространстве. Когда вы смотрите при умеренном ветре на озеро или пруд, обратите особое внимание на то, как ветер влияет на поверхность воды. В любой момент можно увидеть, что одна часть поверхности гладкая, как зеркало, а другую в это же самое время рябит ветер. Более того, в один и тот же момент ветер в разных частях озера будет иметь прямо противоположные направления. Кроме того, эти участки поверхности (где дует ветер) будут постоянно менять очертания и размеры. Теперь представьте себе стрельбище, и вам сразу станет ясно, как причудливо и противоречиво изменяется сила ветра, влияющего на сравнительно низкую траекторию при стрельбе лежа. Для того чтобы лучше представить себе поведение ветра на небольшой высоте над поверхностью земли, понаблюдайте когда-нибудь за кромкой надвигающегося тумана или низко стелющимся облаком. В нескольких футах над землей туман движется самым беспорядочным образом, наступая, отступая, поднимаясь, опускаясь и свиваясь под действием слабого ветра, который, казалось, ведет себя одинаково в разных местах кромки тумана. Стоя лицом к ветру, который дует с большой скоростью, тоже можно ощущать его непостоянство. Задача стрелка в том, чтобы произвести выстрел в момент, когда ветер в наименьшей степени может влиять на движение пули от дульного среза ствола винтовки до мишени. Сейчас мы поговорим о том, какими возможностями располагает для этого стрелок. "Каким бы индикатором ни пользовался стрелок, ему нужно помнить давно проверенное правило: наиболее важной является ветровая обстановка в пределах приблизительно первой трети пути полета пули. Это было установлено в условиях, когда ветровая обстановка создавалась искусственно на разных участках полета пули. Проводились контрольные стрельбы из малокалиберных винтовок, закрепленных в станке, причем все отстрелы для каждой винтовки выполнялись патронами одной и той же партии. Сначала велась стрельба при полном отсутствии ветра, затем она повторялась, но при этом с помощью специальной установки создавался ветер слева со скоростью 50 км в час; ветер создавался на последних 18 метрах полета пули (от 32-го до 50-го метра). После этого стрельба повторялась еще раз в тех же самых условиях, за исключением того, что установка создавала ветер на первой трети пути (от нулевого до 18-го метра). Результаты были очень убедительными. Влияние ветра на последней трети пути пули было ничтожно; на первой трети ветер влиял в наибольшей степени. Ветер, созданный около самих мишеней, смещал среднюю точку попадания очень мало, в то время как ветер около дула винтовки сдвигал средние точки пробоин на несколько дюймов. Вывод: учитывая ветер, следует в основном наблюдать за первой третью стрельбища (от линии огня). Индикаторы ветра должны находиться именно здесь, так как именно на этом участке ветер в наибольшей степени влияет на траекторию полета пули. Обычно именно на этом участке и бывают установлены флажки. Однако, если возможно, наблюдайте и за другими индикаторами. Несколько флажков лучше, чем один, еще лучше флажок в сочетании с листьями, травой и другими индикаторами. 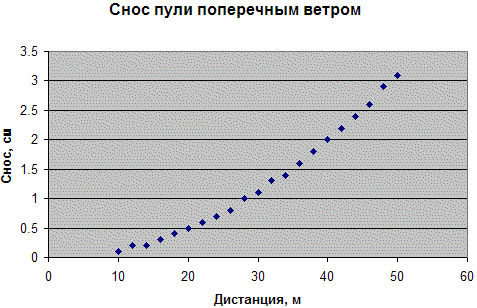 Попробуем посчитать во сколько раз снос пули ветром на первой трети дистанции "сильнее" сноса на последней трети пути в таком эксперименте. Для этого надо вспомнить, что смещение пули на достаточно близком расстоянии пропорционально квадрату пройденного пути, т.е. если, например, на расстоянии в 25м пулю снесло на 1см, то на 50м ее снесет на (50/25)^2 * 1см = 4см. Попробуем посчитать во сколько раз снос пули ветром на первой трети дистанции "сильнее" сноса на последней трети пути в таком эксперименте. Для этого надо вспомнить, что смещение пули на достаточно близком расстоянии пропорционально квадрату пройденного пути, т.е. если, например, на расстоянии в 25м пулю снесло на 1см, то на 50м ее снесет на (50/25)^2 * 1см = 4см.
Ландау бы пояснил это примерно следующими словами: "Из правила Дидиона* о сносе пули очевидно, что смещение пропорционально квадрату пройденного пути", и действительно, это можно легко показать аналитически, но чтобы не углубляться в математические выкладки, возьмем просто баллистический калькулятор и пусть он нам посчитает снос сам. Например, можно взять БК Пропрока и посчитать снос для каких-нибудь значений скорости ветра и баллистического коэффициента - фактические значения этих параметров нас пока не интересуют - главное, нам нужно убедиться в квадратичной зависимости.**** Например, видно, что смещение на 20м равно 0.5 см. Тогда, если квадратичная зависимость верна, то на расстоянии в 40м, смещение должно быть в 4 раза больше, т.е. 2см. Это совпадает с табличным значением. Все остальные значения тоже подчиняются этой зависимости достаточно хорошо с точностью до ошибок округления. 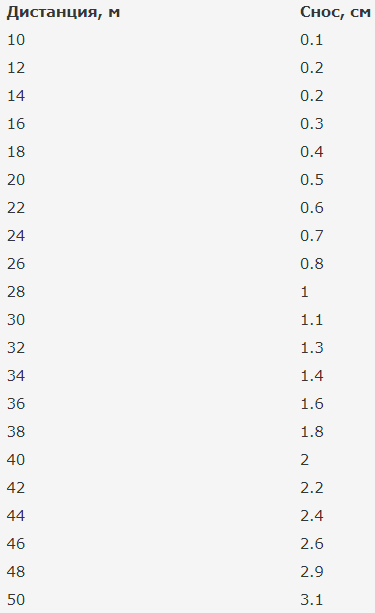
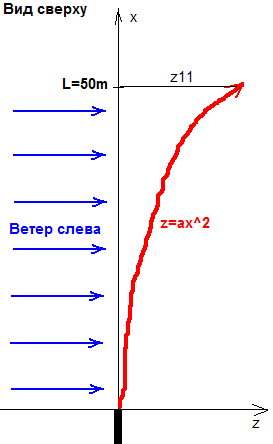
рис.1 Таким образом, мы можем записать, что смещение по оси z пропорционально x^2 или в виде функции: z = a* x^2, где a- постоянный для данного ветра и данной пули коэффициент. На рис.1 показана ситуация, где постоянный ветер дует слева на всей дистанции L. Поэтому смещение пули у цели будет равно:
z11 = a * L^2 Здесь красная линия имитирует траекторию пули, если смотреть на нее сверху. Синие стрелки- ветер. По оси z мы откладываем боковое смещение, а по оси х - расстояние до цели. | 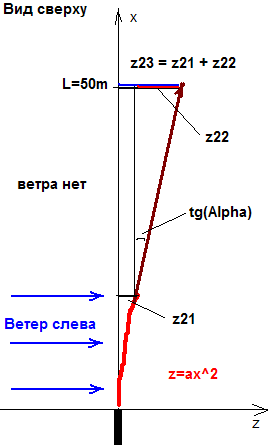 рис.2 рис.2
Теперь посчитаем смещение пули (z23) в ситуации, когда ветер дует лишь на первой трети дистанции. Это смещение будет равно сумме смещений на первой трети расстояния z21( где дует ветер) и на оставшихся двух третях z22 (где пуля летит по прямой, т.к. здесь ветра нет и соответственно нет никаких боковых сил). Очевидно, что z21 = a * (L/3)^2 = a* L^2 /9 Из прямоугольного треугольника мы видим, что
z22 = 2/3L * tg(Alpha), где Alpha - это угол под которым пуля летела в точке x= L/3. Этот угол равен производной функции z(x) в точке x= L/3. tg(Alpha) = dz/dx = d ( ax^2) / dx = 2*a*x = 2/3 * a*L Таким, образом,
z23 = z21 + z22 = a* L^2 /9 + 2/3L* 2/3*a*L = 5/9 * a*L^2 | 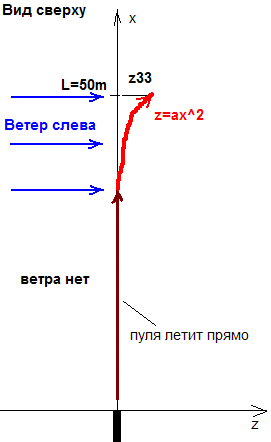
рис.3 На рис.3 мы видим ситуацию, когда вначале нет ветра и пуля летит прямо вплоть до расстояния в 2/3L. Затем "включается" ветер, который снесет пулю на расстояние z33, которое в свою очередь очевидно равно**: z33 = a* (L/3)^2 = 1/9 * a*L^2 |
Ввод: Итак, мы получили, что когда ветер дует только на первой трети дистанции, то снос будет равен 5/9 * a*L^2 и что, снос будет равен 1/9 * a*L^2, если этот же ветер будет "действовать" только на последней трети траектории.
Т.е. различие будет в пять раз! Несмотря на то, что наши расчеты подтверждаются результатом эксперимента, поставленного авторами вышеупомянутой книги, хочется сказать следующее: Ветер сносит пулю сильнее там, где скорость пули меньше и где скорость ветра выше. Думаю, читатель легко теперь сможет подсчитать, где будет больше смещение в следующем эксперименте***: Пусть сначала на первой трети пути дует ветер 1м/c, а дальше ветра нет. А затем, наоборот, вначале пути ветра нет, а на последней трети дует ветер 5м/c. Следуя, совету из книги, стрелок должен был бы сказать, что в первом случае влияние ветра намного больше, вдумчивый читатель не будет столь категоричен:) без проведения небольших расчетов, подобных тем, что мы проделали выше. Еще интересно отметить, что в случае когда ветер дует только на первой трети пути смещение пули равно 5/9 (т.е. чуть больше 50%) от смещения, которое бы получилось, если бы ветер дул на всей дистанции. * Правило Дидиона гласит, что снос пули равен z = Vo * ( t - L/Vo), где t - фактическое время подлета пули к цели на расстоянии L
** На самом деле, скорость пули будет несколько меньше Vo, поэтому смещение z33 будет несколько больше, чем 1/9, но для наших целей, мы этим можем для простоты пренебречь.
*** Здесь надо будет учесть, что сама константа а линейно зависит от скорости ветра, т.е. a ~ u
**** Квадратичная зависимость действует на тех расстояниях, где пуля еще не успевает набрать значительную поперечную составляющую скорости. Это всегда выполняется для пневматических пулек, но неверно для "огнестрельных" пуль, летящих на значительные расстояния, где пуля успевает набрать почти полную поперечную скорость ветра и летит уже по прямой под постоянным углом к линии стрельбы. |

