Как летит пуля. Стабилизирующее вращение и сила МагнусаНазвание документа «Как летит пуля» может показаться странным вопросом, и с первого взгляда может показаться глупым. Тем не менее, как и во многих областях науки и техники, изучение относительно простых вещей более тщательным образом может пролить свет на более сложные и запутанные факты. 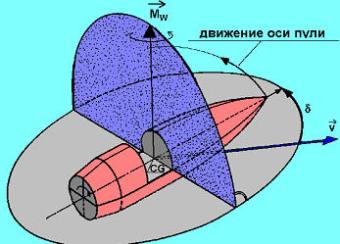 Это особенно верно в отношении движения стабилизируемых вращением пуль, выстрелянных из стрелкового оружия. Большинство людей полагает, что пули летят носиком вперед и остаются стабилизированными от дула до мишени, но это не обязательно так. На коротких дальностях большинство траекторий можно аппроксимировать до прямых линий, в то время как для больших дальностей необходимо принимать в расчет изгиб траекторий. Большинство экспертов по стрелковому оружию принимают тот факт, что пули может болтать, когда они задевают какие-то объекты, или когда они пролетают промежуточные мишени. Тем не менее, как будет выяснено, некоторые физические условия должны быть выполнены для того, чтобы гарантировать стабильный полет, и пуля не будет стабилизироваться автоматически. Закручивание пули наделяет ее гироскопическими свойствами, которые очень важны – но не достаточны – для обеспечения стабильности пули. Тем не менее, с точки зрения преподавания, движение вращающегося гироскопа является одним из наиболее сложных движений, с которым студенты-физики не дружат во время лекций по классической механике. Хотя движение гироскопов в целом может быть описано и полностью понято только путем тщательных математических расчетов, это вступление делает попытку описать элементы этого предмета посредством большого количества иллюстраций. Использование формул ограничено и предназначено только для тех, кто бы хотел их видеть Для объяснения некоторых основных физических терминов, используемых в статье, интересующийся читатель может обратиться к учебнику по элементарной физике. 
Оболочечная пуля калибра .308 Винчестер (7.62 x 51 НАТО) летит со скоростью примерно 2800 фт/с (850 м/с).
Отметьте изменение типа потока от ламинарного к турбулентному на каннелюре пули. Можно различить по крайней мере три ударные волны. Первая и наиболее интенсивная исходит от носика пули и называется конусом Маха. Вторая ударная волна начинается от расположения каннелюры, и третья ударная волна формируется за донцем пули. Кроме того, можно увидеть высоко турбулентный поток позади донца, который называется турбулентный след. Тип потока на поверхности пули изменяется от ламинарного пограничного слоя в переднем регионе пули, который характеризуется параллельными обтекающими линиями, до турбулентного потока, демонстрирующего завихрения, начинающиеся от каннелюры.
Теневая фотография демонстрирует поле обдувания пули, в основном состоящее из ламинарной и турбулентной областей. Поле обдувания в частности зависит от скорости, с которой движется пуля, формы пули и качества ее поверхности, как от наиболее важных факторов. Поле обдувания, очевидно, стремительно изменяется, когда скорость падает ниже скорости звука, которая составляет около 115 фт/с (340 м/с) для стандартных атмосферных условий.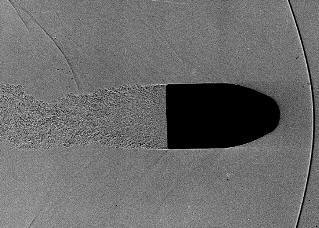 
9-мм оболочечная пистолетная пуля (9 mm Luger FMJ), летящая немного быстрее скорости звука.
Можно заметить серьезные отличия: конус Маха все еще присутствует, но он больше не прикреплен к носику пули, и угол открытия конуса увеличился. Турбулентный след все еще виден, но пограничный слой является ламинарным от носика до донца, на всем протяжении поверхности пули.
Пистолетная пуля калибра .32 ACP (7.65 мм Браунинг), летящая на скорости, намного меньшей скорости звука. За донцем пули можно наблюдать только турбулентность (слабую).
Математические формулы, посредством которых можно определить параметры поля обдувания (к примеру, давление и скорость поля обдувания в каждом положении) хорошо известны в математике, как уравнения Навье-Стокса. Тем не менее, данные уравнения и их действительные корни являются совершенно различными вещами. Даже с помощью мощных компьютеров до сих пор удалось найти всего лишь несколько применимых решений для некоторых специфических конфигураций. В виду таких математических ограничений баллистики по всему миру рассматривают движение пули в атмосфере, не учитывая специфических характеристик поля обдувания, и применяя упрощенную точку зрения: поле обдувания характеризуется силами и моментами, действующими на тело. В общем случае, эти силы и моменты должны быть определены экспериментально, что осуществляется в процессе стрелковых экспериментов и тестированием в аэродинамических трубах.
В общем случае, тело, движущееся через атмосферу, подвергается влиянию различных сил. Некоторые из этих сил являются силами массы, и прикладываются к СG (центру тяжести) тела и зависят от массы тела и ее распределения по телу. Вторая группа сил называется аэродинамическими силами. Эти силы происходят от взаимодействия поля обдувания с пулей и зависят от формы и качества поверхности тела. Некоторые аэродинамические силы зависят от рыскания, либо от вращения, либо от обоих из них. Так как мы пытаемся изучать движение пуль на Земле, нам необходимо принимать во внимание ее вращение. Тем не менее, формулы Ньютона для движения справедливы только в инерциальной справочной системе координат – которая либо покоится, либо движется с постоянной скоростью. Поскольку мы считаем, что пуля движется в справочной системе координат, закрепленной на вращающейся Земле, нам приходится иметь дело с системой координат, движущейся с ускорением. Но мы можем компенсировать это – и все еще использовать формулы Ньютона – добавлением двух дополнительных сил. Очевидно, что опрокидывающий момент стремиться увеличить угол рыскания, и можно ожидать, что пуля начнет болтаться и станет нестабильной. Это хорошо видно, если стрелять пулями из стволов, не имеющих нарезов. Тем не менее, если мы говорим о вращающихся снарядах, в игру вступает гироскопический эффект, влияние которого невероятно. Гироскопический эффект может быть описан и объяснен исходя из общих законов физики и может быть подтвержден математическими вычислениями. В данный момент мы просто должны принять то, что мы наблюдаем: ввиду гироскопического эффекта продольная ось пули движется в противоположном направлении от опрокидывающего момента, как показано стрелкой на рисунке. В общем случае из-за влияния гироскопического эффекта, ось симметрии пули будет двигаться по поверхности конуса со скоростью, вектор которой будет направлен по оси конуса. Это движение часто называется прецессией. Тем не менее, более современные источники называют это медленной модой осцилляции. Опрокидывающий момент стремиться повернуть пулю вокруг оси, которая проходит через CG и которая перпендикулярна плоскости рыскания, плоскости, сформированной вектором скорости v и продольной осью пули. При отсутствии вращения угол рыскания d будет возрастать, и пуля начнет болтаться. Если пуля обладает существенным вращением, скажем, если она вращается достаточно быстро вокруг оси своей симметрии, будет иметь место гироскопический эффект: продольная ось пули движется в направлении опрокидывающего момента, перпендикулярно к плоскости сопротивления. Тем не менее, эта ось смещается вместе с плоскостью сопротивления, которая затем поворачивается вокруг вектора скорости. Чтобы еще больше все усложнить, скажем, что реальное движение стабилизируемой вращением пули еще более запутано. В дополнение к этому, к медленной осцилляции добавляется еще и быстрая осцилляция. Поверхностное трение на поверхности пули замедляет ее вращательное движение. Момент затухания вращения (также момент затухания оборачивания) рассчитывается по приведенной выше формуле. Коэффициент затухания вращения зависит от геометрии пули и типа обтекания (ламинарное или турбулентное). В общем случае ветровая нагрузка будет являться доминирующей аэродинамической силой. Тем не менее, существует еще несколько более мелких сил, но нам бы хотелось упомянуть только силу Магнуса, которая, как оказывается, является очень важной для стабилизации пули.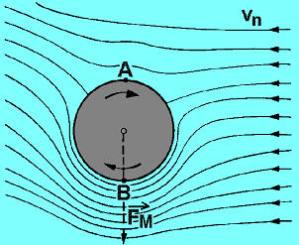 В соответствии с рисунком 5 , мы рассматриваем пулю сзади. Предположим, что пуля имеет правостороннее вращение, как показано двумя стрелками. Кроме того, мы предусматриваем наличие угла рыскания d. Продольная ось пули должна наклоняться влево, как показано на предыдущих рисунках. И еще существует компонент скорости ветрового потока Vn, перпендикулярный оси симметрии пули. Из-за вращения пули и прилипания молекул воздуха к поверхности пули, ветровой поток в районе пули становится асимметричным. Скорость течения воздуха и скорость поворота тела вычитаются в точке А и складываются в точке В (смотри приведенный выше рисунок). Тем не менее, в соответствии с правилом Бернулли (смотри любой учебник по элементарной физике), это совпадает с различием в давлении. Повышенное давление в А и пониженное давление в В дает увеличение направленной вниз силы, которая также называется силой Магнуса , приводящей к возникновению направленной вниз (только для данной диаграммы!) Это объясняет то, почему сила Магнуса, в отношении летящей пули, требует наличия вращения, а также угла рыскания, иначе она исчезает. Теперь мы закончили обсуждать наиболее важные силы и аэродинамические моменты, влияющие на движение пули, но пока мы не видели, как выглядит результирующее движение пули. В данный момент нас не интересует сама по себе форма траектории (поступательное движение тела), но мы хотим сконцентрироваться на вращении вокруг ЦТ. Рыскающее движение пуль, стабилизируемых вращением, производимое суммой всех аэродинамических моментов, может быть смоделировано в виде суперпозиции быстрой и медленной мод осцилляции, и наиболее простым образом может быть объяснено и понято посредством двухплечевой модели. 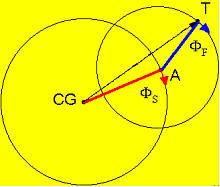 Представьте себе, что вы смотрите на пулю сзади, как показано на рисунке. Простая двухплечевая модель адекватно описывает рыскающее движение пули, стабилизированной вращением, происходящее от взаимодействия всех аэродинамических моментов.
Рыскающее движение может быть осознано как суперпозиция быстрой и медленной осцилляций, часто называемых нутацией и прецессией. Представьте, что вы смотрите на пулю сзади. Плечо медленной моды от CG до A должно иметь точкой вращения CG и вращается с частотой медленной моды. Таким образом, А движется по окружности вокруг (красная окружность). Плечо быстрой моды от A до T, где T – носик пули, должно иметь точкой вращения точку А и вращаться с частотой быстрой моды. Таким образом, T вращается по окружности вокруг А. Расстояние от CG до T – это проекция продольной оси пули. В соответствии с рисунком, представьте, что вы смотрите на пулю, летящую в сторону глаза наблюдателя. Тогда носик пули движется по спиралевидной (она еще называется геликоидной) траектории, как показано на рисунке, в то время, как CG остается закрепленным в центре окружности. Носик пули периодически возвращается назад, перпендикулярно к траектории. Если это происходит, угол рыскания становится минимальным. 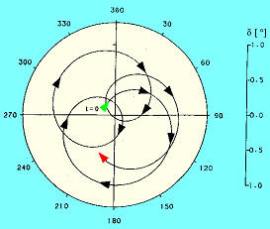 Данный рисунок схематически показывает основное угловое движение пули, стабилизированной вращением, вблизи от дульного среза. Представьте, что CG пули закреплен в центре системы координат, и таким образом, пуля летит в направлении глаза наблюдателя. Тогда ее носик движется по спиралевидной траектории (как показано кривыми линиями) в направлении стрелок. На дульном срезе (t=0) угол рыскания может быть маленьким, но возрастать до максимального значения примерно в 1°, уменьшаясь затем снова почти до нуля.
Отметьте, что величина успешных максимальных углов рыскания будет меньше, чем у их предшественников, так как пуля на рисунке предполагается динамически стабильной (максимальный угол рыскания уменьшается по мере того, как пуля продолжает продвигаться вперед). Эта простая модель адекватно описывает рыскающее движение, если дополнительно принять, что частота быстрой моды превосходит частоту медленной моды, и длины плеч для медленной моды и быстрой моды для динамически стабилизированной пули постоянно укорачиваются. Говорят, что стабилизируемый вращением снаряд гироскопически стабилен, если, при наличии угла рыскания d, он отвечает на внешнюю ветровую нагрузку F1 основным движением нутации и прецессии. В этом случае продольная ось пули движется в направлении, перпендикулярном направлению ветровой нагрузки. Можно показать путем математических выкладок, что это условие выполняется, если фактор гироскопической стабильности sg превосходит единицу. Такое состояние называется условием гироскопической стабильности. Пулю можно сделать гироскопически стабильной путем ее существенной раскрутки. (при увеличении w!). ак как частота вращения w уменьшается намного медленнее, чем скорость vw, фактор гироскопической стабильности sg, как минимум вблизи от дульного среза, постоянно возрастает. Практический пример показан на рисунке 10 Этот рисунок демонстрирует фактор гироскопической стабильности для пули М80 калибра 7.62 x 51 НАТО, выстреленных под углом вылета 32° со скоростью 870 м/с из ствола с шагом нарезов в дульной части в 12 дюймов. Пуля M80 демонстрирует статическую стабильность на всем протяжении траектории полета, так как условие статической стабильности sg>1 сохраняется везде. Величина sg имеет минимальное значение 1.35 на дульном срезе. В общем можно сказать, что если пуля статически стабильна на дульном срезе, то она будет статически стабильно на всем оставшемся полете. Это можно просто понять из того факта, что фактор статической стабильности пропорционален отношению вращательной и поперечной скоростей пули (смотри формулу ). Так как скорость вращения пули затухает намного меньше, чем поперечная скорость (которая затухает вследствие действия силы сопротивления воздуха), фактор статической стабильности возрастает, по крайней мере, на большей части. Конструктора пуль и винтовок обычно предпочитают sg > 1.2 ..1.5 на дульном срезе, тем не менее, можно заметить, что многие образцы стрелкового оружия демонстрируют избыточную статическую стабильность. Так, если пуля гироскопически стабильна на дульном срезе, она будет гироскопически стабильна на всем остальном полете. Величина sg также зависит от плотности воздуха r и поэтому необходимо уделять большое значение гарантированной гироскопической стабилизации пули в условиях экстремально холодных температур. Конструктора пуль и оружия обычно предпочитают иметь sg > 1.2...1.5, но также возможно достигать еще большей стабилизации. Это называется перестабилизацией. Фактор гироскопической (также он называется статической) стабильности зависит всего от одного аэродинамического коэффициента (производного коэффициента опрокидывающего момента cMa) поэтому его определять намного проще, чем фактор динамической стабильности. Это может быть причиной, по которой некоторые публикации по баллистике приводят только статическую стабильность, когда упоминается стабилизация пуль. Тем не менее, условие гироскопической стабильности является всего лишь необходимым условием, гарантирующим стабильный полет, но не самым существенным. Два других условия – условие динамической стабильности и условие податливости также должны быть удовлетворены. Говорят, что снаряд динамически стабилен, если его нутация и прецессия со временем гасятся, что говорит о том, что его угол рыскания, получаемый при вылете за пределы дульного среза (первоначальное рыскание) уменьшается. Фактор динамической стабильности +* может быть определен из линеаризованной теории гироскопов (предполагая, что углы рыскания малы) и из приведенного выше условия динамической стабильности. Иная трактовка этого условия осуществляется на основании треугольника стабильности. Если, наоборот, пуля динамически нестабильна, угол рыскания увеличивается. Появление начального угла рыскания на дульном срезе вовсе не является индикатором нестабильности пули. В некоторых последних публикациях утверждения «пуля не стабилизирована» и «пуля показывает (большой) угол рыскания» используются как синонимы, что неверно. Наоборот, начальный угол рыскания на дульном срезе неизбежен и происходит из-за различных возмущений. Пули, выстреленные из стрелкового оружия, автоматически не будут динамически стабильны. Пули могут быть динамически нестабильны в момент вылета из ствола. Другие пули динамически стабильны около дульного среза и теряют динамическую стабильность по мере продолжения полета, когда поле обдувания начинает изменяться. Равновесный угол рыскания (или рыскание покоя, также называемое равновесным рысканием) – это угол, на который отклоняется мгновенная ось прецессии от направления полета (см. рис). В результате влияния этого маленького наклона, возникает постоянный воздушный поток, который стремится отклонить пулю вправо. Таким образом, возникновение рыскания покоя является причиной, по которой пуля отклоняется вправо (для правосторонних нарезов) или влево (для левосторонних нарезов). 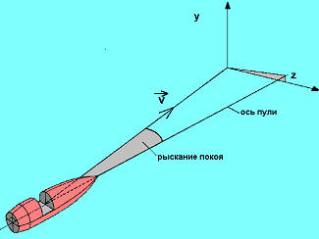 Поскольку мгновенное рыскание, получаемое на дульном срезе, у стабильной пули гасится, угол d становится равным рысканию покоя. Величина угла рыскания покоя обычно составляет лишь доли градуса около дульного среза, но может достигать существенных значений в верхней точке траектории, особенно для больших углов вылета.
Возникновение рыскания покоя ответственно за боковой снос стабилизируемых вращением снарядов даже при отсутствии ветра. Зависящий от вращения боковой снос также называется деривацией. Также можно показать, что для правостороннего вращения рыскание покоя лежит справа от траектории. Таким образом, носик пули описывает розочку со средним смещением вправо, что приводит к боковому сносу вправо. Для пули с правосторонним вращением ось симметрии пули в основном направлена вправо и немного вверх по отношению к 35 направлению вектора скорости – указывающего направление, в котором движется ЦТ – так как показано на рисунке. Если пуля летит стабильно (гироскопически и динамически!) и случайное рыскание погашено, обычно после пролета дистанции в несколько тысяч калибров, ось симметрии пули и перпендикуляр к траектории расходятся на небольшой угол, и тогда говорят о наличии рыскания покоя . Для пуль, выстреленных из стволов с правосторонними нарезами, продольная ось смещается вправо и немного вверх по отношению к направлению полета, приводя к боковому сносу вправо. Рыскание покоя, хотя оно обычно измеряется лишь долями градуса, является причиной сноса пуль, стабилизируемых вращением.
Как уже говорилось, о статической нестабильности обычно беспокоиться не приходится, если иметь дело с хорошо сконструированной пулей, выстреленной из стрелкового оружия. Тем не менее, результаты экспериментальных исследований Джилза и Лиминга (смотри Вывод) для пуль 7.62 x 51 НАТО, выстреленных из гладкого ствола, могут быть расширены, как минимум, в некоторой степени, до послерикошетного полета нестабилизированных снарядов. В своих экспериментах Джилз и Лиминг определили «отсутствие признаков чистого опрокидывания с одного конца на другой» и то, что такие невращающиеся пули НАТО летели «примерно широкой стороной вперед» и «просто колебались по сторонам в направлении запуска, а затем быстро затухали в уравновешенном положении при большом угле рыскания». Авторам даже удалось оценить стационарный угол рыскания теоретическим путем, применив аналогию поперечного потока, и определить, что статически нестабильная пуля НАТО летит донцем вперед при стационарном угле рыскания примерно в 127°. На рисунке показано рыскающее движение пули Wadcutter калибра .38 Special, выстреленной из револьвера. Пуля статически стабильна, фактор статической стабильности, больший четырех, говорит о том, что пуля закручена слишком сильно. Очевидно, что пуля динамически нестабильна. Осцилляция на медленной моде постоянно возрастает. Максимальный угол рыскания увеличивается примерно в три раза от значения в пять градусов на дульном срезе до 15° после прохождения дистанции в 8000 калибров (240 футов = 73 м). Возникает вопрос, в каких случаях эти нестабильности имеют существенный практический эффект. Если говорить о коротких дистанциях до нескольких тысяч калибров, динамическую нестабильность пули определить трудно, если, конечно, не применять очень сложную технику измерений. Если пуля сильно превышает эту дальность, угол рыскания достигает существенных значений, сопротивление возрастает и кучность падает. Скорее всего, вариации от выстрела к выстрелу будут ненормальными, а траектории станут непредсказуемыми. Измерение скорости Доплеровским радаром для стандартной пули НАТО калибра 7.62x51, выстрелянной под углом 38.7° демонстрирует быструю потерю скорости вблизи дульного среза, но осциллирующую природу скорости для полетного времени, превышающего 14 секунд. Считается, что такая осцилляция скорости с частотой 1.0...1.6 Гц может быть объяснена прецессионной нестабильностью, приводящей к конусообразному движению пули. С первого взгляда все выглядит нормально. Скорость пули существенно уменьшается вблизи дульного среза, и после общего времени полета примерно в 30 секунд, пуля падает на дальности более 2,5 километров. Более пристальное изучение кривой зависимости скорости от времени, начиная с 14 секунд полета, четко демонстрирует осциллирующее поведение. Увеличенный сектор кривой зависимости скорости от времени показан на нижней иллюстрации рисунка. Расчеты показывают, что частота колебания скорости возрастает от примерно одного оборота в секунду на 20 секундах полетного времени до почти двух оборотов в секунду на 28 секундах. Нет никаких сомнений в том, что измерения при помощи Доплеровского радара не являются ошибочными. С другой стороны, мы столкнулись не с аэродинамической силой, которая может быть ответственна за ускорение или замедление пули и вызывать осцилляции скорости. Это экспериментальное наблюдение можно объяснить динамической нестабильностью пули 7.62 х 51 НАТО на низких скоростях. Из предыдущих рисунков мы узнали, что пуля калибра 7.62 х 51 НАТО статически и динамически стабильна вблизи дульного среза. Таким образом, рыскающее движение будет затухать, и после пролета определенной дистанции рыскание, за исключением небольшого рыскания покоя (деривации), практически окажется нулевым.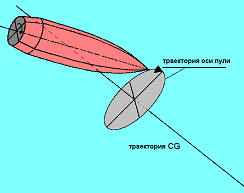 Когда скорость пули существенно снизится, и она начнет лететь на дозвуковой скорости, спектр обтекания сильно изменится. Это было подтверждено экспериментальными исследованиями BRL (смотри Выводы), и одним из последствий изменения спектра обтекания станет смещение центра давления для силы Магнуса. Для сверхзвуковой скорости эта точка располагается позади ЦТ, но перемещается вперед ЦТ на дозвуковых скоростях. Как было показано ранее (смотри рисунок 7 ), момент Магнуса становится сильным дестабилизирующим моментом, и как следствие, пуля становится динамически нестабильной. Осцилляция на низких частотах, также называемая прецессией, больше не будет угасать и начинает медленно усиливаться. Тем не менее, пуля все еще имеет повышенную статическую стабильность, и, таким образом, гироскопический эффект продолжает иметь место. В конце концов, продольная ось пули смещается к поверхности конуса, в то время, как траектория является осью конуса. Так как эта осцилляция незатухающая, угол открытия конуса постоянно возрастает. Рисунок 26 схематически показывает конусообразное движение пули НАТО на ниспадающей ветви траектории. Очевидно, что динамическая нестабильность пули НАТО оказывает заметное влияние на ее траекторию. По мере увеличения рыскания, скорость пули еще больше уменьшается, и дальность падает. Было отмечено, что для изучаемой партии пуль НАТО нестабильности были не воспроизводимы, и дальности, таким образом, даже при стрельбе на практически одинаковых дульных скоростях и при практически одинаковых углах вылета отличались существенно, по случайному закону. Стоит еще отметить, что расчеты внешней баллистики (смотри Выводы), основанные как на модели точечной массы, так и на модифицированной модели точечной массы не способны точно предсказать траекторию такой нестабильной пули. Пуля вылетает из ствола в неподвижную воздушную среду, т.е. воздух стоит на месте и бокового ветра нет. В горизонтальной плоскости все физические свойства гиростабилизированной пули имеют одинаковое значение относительно траектории ее полета. Углы рыскания влево и вправо одинаковы и компенсируют друг друга. Учитывая уменьшение этих углов по мере движения по траектории, мы можем принять, что пуля летит строго по линии вращения. Эта линия задана первоначально стрелком при выстреле. Так она и будет лететь пока нет бокового ветра. Центр давления или максимального сопротивления набегающего потока воздуха находится впереди центра тяжести и располагается на линии полета. Пуля как бы закреплена в этом центре давления. Далее появляется боковой ветер. Он осуществляет смещение вбок конуса ударной волны и через центр давления старается повернуть носик пули относительно центра тяжести. Дополнительно появляется набегающий поток воздуха внутри конуса ударной волны, который добавляет дополнительное отклонение по аналогии с подъемной силой крыла самолета на сверхзвуке. Гироскоп, который представляет пуля, тут же старается вернуть ось своего вращения к ориентации, которая была до возмущения. Этот возврат происходит не центром давления, а центром тяжести. Пуля занимает первоначальное положение немного в стороне от прежней линии полета. Мы знаем, что у гироскопа ось вращения уходит не по прямой от линии давления бокового воздуха, а и дополнительно отклоняется либо вверх, либо вниз, в зависимости от направления ветра. Это дополнительное отклонение так же приходит в ноль за счет гироскопического эффекта. В итоге пуля займет свою первоначальную ориентацию не только немного в стороне, а и выше, либо ниже. Но ветер снова повторяет отклонение оси вращения пули и пуля снова компенсирует это отклонение гироскопическим эффектом. Так и идет борьба между боковым ветром и гироскопическим эффектом. Как только ветер прекратится, этой борьбы не будет и пуля продолжит свой полет в той ориентации, которую обеспечивает гироскопический эффект. Что касается набегающего потока воздуха внутри конуса ударной волны. При любом отклонении оси вращения, пуля перейдет, как вы сказали, в "мелкопериодические колебания". Набегающий поток будет не только с одной стороны, а и с противоположной. Сила его не одинакова слева и справа, поэтому в совокупности с основной силой отклонения ветром, появится некий малый угол. Считается, что при боковом ветре в 20 миль в час центральная линия пули наклонится на угол 0,52 градуса относительно направления полета. Такой маленький и даже больший угол очень трудно заметить среди отклонений точек попадания пуль.
Выводы:
Пули, выстрелянные из стрелкового оружия, следуют общим правилам физики и ведут себя, как гироскопы. Угловое движение этих пуль может быть представлено в виде двух осцилляций, которые проще всего можно показать на двухплечевой модели. Практически все пули для стрелкового оружия являются статически стабильными, многие пистолетные и револьверные пули даже имеют избыточную статическую стабильность. Тем не менее, динамическая стабильность не является автоматически гарантированной. Некоторые пули динамически нестабильны в момент вылета из канала ствола, другие могут терять динамическую стабильность во время полета после такого как подвергаются замедлению. До настоящего времени не существует иного удобного метода, кроме эксперимента, с помощью которого можно предсказать динамическую нестабильность пули, особенно на дальних дистанциях. Некоторые очень сложные компьютеризованные процедуры (численные решения формул Навье-Стокса) для решения этих проблем только разрабатываются исследователями-баллистами. Автор: Ruprecht Nennstiel (скачать книгу полностью) |
